MEDIDAS DE DISPERSION

El rango semi-intercuartil o desviación cuartil de un conjunto de datos se determina mediante la siguiente expresión:

Rango percentilar

El rango percentilar 10-90 de un conjunto de datos se define

rango percentil 10-90=P90-P10

Desviación estándar

La desviación estándar de un conjunto de n de números x1, x2, ... xn se denota por S

donde x representa las desviaciones de cada uno de los números xj, respecto de la Xmedia. Por lo tanto S es la media cuadrática de las desviaciones en relación con la media o, como se le llama en forma común desviación de la media cuadrática.

Ejemplo.

Calcule el rango de los conjuntos, la desviación media

a) 12, 6, 7, 3, 15, 10, 18, 5

b) 9, 3, 8, 8, 9, 8, 9, 18

a) S=4.25
b) S=2.125

Tarea de desviacion estandar

Desviación estándar

La desviación estándar (o desviación típica) es una medida de dispersión para variables de razón (ratio o cociente) y de intervalo, de gran utilidad en la estadística descriptiva. Es una medida (cuadrática) que informa de la media de distancias que tienen los datos respecto de su media aritmética, expresada en las mismas unidades que la variable.

Para abordar las cuestiones que comentábamos en el párrafo anterior, nos valemos de herramientas como la varianza y la desviación estándar. Ambas medidas están estrechamente relacionadas ya que definimos una a partir de la otra.

Para conocer con detalle un conjunto de datos, no basta con conocer las medidas de tendencia central, sino que necesitamos conocer también la desviación que representan los datos en su distribución respecto de la media aritmética de dicha distribución, con objeto de tener una visión de los mismos más acorde con la realidad a la hora de describirlos e interpretarlos para la toma de decisiones.

La varianza representa la media aritmética de las desviaciones con respecto a las media elevadas al cuadrado. Si atendemos a la colección completa de datos (la población en su totalidad) obtenemos la varianza poblacional; y si por el contrario prestamos atención sólo a una muestra de la población, obtenemos en su lugar la varianza muestral.

El término desviación estándar fue incorporado a la estadística por Karl Pearson en 1894.

Por la formulación de la varianza podemos pasar a obtener la desviación estándar, tomando la raíz cuadrada positiva de la varianza. Así, si efectuamos la raíz de la varianza muestral, obtenemos la desviación típica muestral; y si por el contrario, efectuamos la raíz sobre la varianza poblacional, obtendremos la desviación típica poblacional.

Cuartiles, Deciles y perceptiles

Encuentre:
a) Los cuartiles Q1, Q2, Q3
b) los deciles D1, D2, D3... D9 para los salarios de la empresa Pr.

Salarios No. de empleados

$250.00-$259.99 8

$260.00-$269.99 10

$270.00-$279.99 16
$280.00-$289.99 14
$290.00-$299.99 10
$300.00-$309.99 5
$310.00-$319.99 2
Total: 65

El primer cuartil Q1 es el salario obtenido contando N/4=65/4. De los casos empezando con la primera clase (inferior). Ya que la primera clase incluye 8 casos, debemos tomar 16.25-8=8.25 de los 10 casos de la segunda clase. Por el método de interpolación lineal se obtiene Q1= $259.99 + 8.25/8 ($10.00)= $268.25
El segundo cuartil Q2 se obtiene contando los primeros 2N/4 = N/2 = 65/2 = 32.5 casos. Dado que las dos primeras clases incluyen 18 casos, habra que tomar 32.5-18=14.5, entonces Q2=269.99+(14.5/16)*10 = $279.06
El tercer cuatil Q3 se obtiene contando los primeros 3N/4= 48.75 casos. Dado que las 3 primeras clases incluyen 34 casos habra que tomar 48.75-34=14.75, entonces Q3=279.99+(14.75/14)*10= $290.52

Por lo tanto 25% de los empleados reciben $268.25 pesos o menos, el 50% reciben $269.06 pesos o menos y 75% reciben $290.75 o menos.

REPASO DE LA UNIDAD I

Notación sumatoria

Media aritmética

Propiedades de la media aritmética

Mediana

REGRESION LINEAL

Se estudia el ingreso económico mensual de familias dependientes de obreros, residentes. dicho ingreso puede compararse contra la edad del padre de familia, de este modo se estudian 2 variables que representan a su vez una variable susceptible a describirse como un par ordenado estadístico (x,y).
En la tabla siguiente se muestran los datos correspondientes a una muestra aleatoria.

Ingresos mensuales en miles de pesos dependientes de obreros según la edad del padre

Grafica de Ingresos Vs. Edad, linea de tendencia (la pendiente)

FORMULAS QUE SE UTILIZARON:

Y'=a + b(x)

∑Y=n*a + b∑X

∑XY= a*∑X + b∑X2
donde, n= numero de muestras

Calculos Realizados:

∑Y = 195 = (30)*a+(1378)*b

∑XY = 9123.8 = (1378)+(64726)*b

Se utilizo un sistema de ecuaciones simultaneas

Solución:

a= 2.0470

b=0.0974

Sustitucion

Y=a + b(x)
Y'= 2.0470 +0.0974X

Problemas y ejercicios:

Supongamos que el siguiente conjunto de datos en una muestra aletoria de 40 calificaciones de autoconcepto.

100	112	88	105	100	102	98	113
102	87	93	93	117	100	98	92
100	117	97	100	83	67	76	100
106	117	89	83	100	109	109	93
105	108	104	63	81	109	100	98

a) Determine Xmax y Xmin y el rango.

Xmax= 117, Xmin= 63, rango= 54.

b) ¿Cuantos intervalos sugeriría para mostrar la distribución?

Cerca de 10 intervalos a menos que n sea muy grande.

c) Determine el ancho del intervalo, w, para permitir 10 intervalos.

w=rango/10 = 54/10= 5.4, redondeado a 5.

d) Si w=5 ¿cual es el primer intervalo (valores mas bajos)?

El menor múltiplo de 5 que es menor que 63 es 60:60-64

e) Si w= 5, liste los intervalos.

f) Construya una distribución de frecuencias agrupadas para los 40 valores. (Utilice el método de conteo con estacas).

g) Construya columnas de porcentaje y porcentaje acumulado para esos datos.

intervalo	conteo	ƒ	%	% acumulado
60-64	I	1	2.5	2.5
65-69	I	1	2.5	5,0
70-74		0	0,0	5,0
75-79	I	1	2.5	7.5
80-84	I I I	3	7.5	15,0
85-89	I I I	3	7.5	22.5
90-94	I I I I	4	10,0	32.5
95-99	I I I I	4	10,0	42.5
100-104	I I I I I I I I I	11	27.5	70,0
105-109	I I I I I I	7	17.5	87.5
110-114	I I	2	5,0	92.5
115-119	I I I	3	7.5	100,0
		n= 40	100,0

h) ¿Seria un polígono de frecuencias una grafica apropiada para estos datos? ¿Por qué?

Si los polinomios de frecuencia son excelentes para variables continuas.

i) Construya un polígono como el de la figura 2,.4 con estos datos

Frecuencia Vs Punto medio de intervalo

j) Construya una ojiva de esos datos

% acumulado vs limite superior

k) Estime P10 y P50 y P90 utilizando la ojiva.

P₁₀=80; P₅₀=100;P₉₀=110

l) Construya una grafica horizontal de caja y patillas para esto datos. (nota: las graficas de caja pueden tener una orientación vertical u horizontal. para la orientación horizontal, las patillas se extiende a la izquierda y a la derecha de la caja).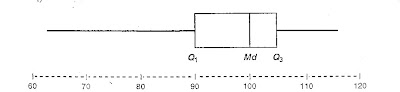

m) Comente sobre la aparente simetría o asimetría de esos datos.

Parece que la distribución es asimétrica y sesgada a la izquierda.

n) ¿Como diferirá una ojiva de asimetría positive de la asimetría negativa?

La ojiva de una distribución asimétrica positiva se elevaría muy rápido de la línea base en el lado izquierdo de la ojiva debido al conjunto de valores en las regiones mas bajas. Por otro lado, la ojiva de una distribución asimétrica negativa no comenzara a elevarse rápidamente sino hasta que alcance los valores altos en el lado derecho de la figura.

o) ¿Puede suponer como podría aparecer la ojiva de una distribución rectangular?

Una línea recta inclinada hacia arriba desde el extremo inferior izquierdo hasta el extremo superior derecho.

2.- El siguiente conjunto de datos es de una muestra aleatoria de 50 casos de los datos del HSB. En este caso, los números representan la raza de los individuos, de donde 1 = hispano, 2= asiático, 3= negro, 4= blanco.

4	1	4	4	1	1	4	4	4	2
4	4	2	4	4	4	3	4	4	4
1	4	4	4	1	4	4	3	4	4
4	3	1	4	4	4	1	3	4	4
4	3	3	4	4	3	3	4	4	4

a) ¿Un polígono de frecuencias es apropiado para graficar esos datos? ¿Por que? No ya que esos datos son categóricos mas que cuantitativamente continuos.

b) ¿Es apropiada una grafica de barras para graficar esos datos? ¿Por que? Una excelente elección, ya que los datos no tienen un continuo fundamental.

c) Construya una distribución de frecuencias agrupadas para estos datos. (Utilice el método de Tukey).

d) Construya una columna de porcentajes para esos datos.

e) Construya un histograma de frecuencias para esos datos.

f) Etiquete el eje vertical de la figura en el e) para indicar frecuencia y porcentajes.

g) ¿Habría probablemente brechas entre las columnas del histograma? ¿Por qué? Si, ya que es congruente con los datos categóricos no clasificables.

Problemas y ejercicios

Los ejercicios del 1 al 10 están basados en los siguientes datos.

En un grupo de sexto grado con 36 estudiante, se administra una tecnica sociométrica de “adivina quien” para evaluar el grado de relaciones positivas entre ellos para cada estudiante. Los valores para los 36 estudiantes fueron:

22	3	12	2	0	7	1	9	1	28	5	2
2	2	33	4	8	13	2	3	1	28	10	14
22	1	4	15	1	52	5	8	3	11	17	1

1.- ¿Cual es el rango?

Rango = X_max-X_min = 52-0 = 52

2.- Construya una distribución de frecuencias no agrupada.

X	ƒ		X	ƒ		X	ƒ		X	ƒ		X	ƒ		X			X	ƒ
52	1		44	0		36	0		28	2		20	0		12	1		4	2
51	0		43	0		35	0		27	0		19	0		11	1		3	3
50	0		42	0		34	0		26	0		18	0		10	1		2	5
49	0		41	1		33	1		25	0		17	1		9	1		1	6
48	0		40	0		32	0		24	0		16	0		8	2		0	1
47	0		39	0		31	0		23	0		15	1		7	1
46	0		38	0		30	0		22	2		14	1		6	0
45	0		37	0		29	0		21	0		13	1		5	2

3.- Construya una distribución de frecuencias agrupada, w= 5.

Intervalo	ƒ		Intervalo	ƒ		Intervalo	ƒ
50-54	1		30-34	1		10.-14	5
45-40	0		25-29	2		5.-9	6
40-44	0		20-24	2		0-4	17
35-39	0		15-19	2

4.-Construya un histograma de esos datos y comente sobre la forma de la distribución.
La distribución es asimétrica y altamente sesgada positivamente

Frecuencia Vs punto medio

5.- Construya una ojiva.

6.- Estime Q1 y Q2.

Q1 = 2 o 3, Q3 = 13.5

7.- Calcule la media.

9.78

8.- Determine la mediana.

5

9.- Determine la moda.

1

10.-Comparte la distancia de Q1 a Q2 con la distancia de Q2 a Q3. El patrón sugiere asimetría.

Q3-Q2 es mayor que Q2-Q1. Positiva.

11.- Para una década reciente, el incremento en el ingreso medio en el sur fue 74 % para blanco y 113 % para no blancos. ¿Cuál es el incremento medio para ambos grupos combinados si de cada 100 trabajadores 82 fueron blancos?

12.-Suponga que siete amigos viven junto a una autopista y quieren juntarse en la casa de uno de ellos para comer tacos y discutir las medidas de tendencia central y sus tipos favoritos de graficas. Si sus casas a lo largo de la autopista están situadas de este a oeste en este orden: A, B, C, D, E, F Y G, ¿Dónde deberían reunirse para minimizar la suma de las distancias recorridas?
Md en el punto D. (La suma de las derivaciones absolutas es un mínimo alrededor de la mediana).

13.- Suponga que una distribución tiene una media de 70, una mediana de 65 y una moda 55. ¿En que dirección esta sesgada la distribución?
Esta sesgada a la derecha, es decir, positivamente.

14.- Si aplica prueba de Cl a una clase en dos ocasiones separadas, como regla general, comente sobre las diferencias relativas entre las dos medias, las dos medianas y las dos modas.
Se espera que las medias difieran menos y que las modas difieran más.

Las preguntas 15-16 corresponden a los datos presentados en la tabla 2.2.
15.- Mo=?
50

16.- Md=?
51